La Derivada

En cálculo (rama de las matemáticas), la derivada representa cómo una función cambia a medida que su entrada cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una cantidad en un punto dado; por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo es la velocidad instantánea con la cual el vehículo está viajando.

La derivada de una función en un valor de entrada dado describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente en la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.

El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.

Supongamos que tenemos una función y la llamamos . La derivada de es otra función que llamaremos .

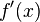representa la pendiente de la recta tangente a la gráfica de en el punto .

En términos geométricos, esta pendiente 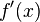es "la inclinación" de la línea recta que pasa justo por encima del punto 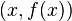y que es tangente a la gráfica de .

Al identificar dos puntos muy cercanos en la gráfica y al unirlos mediante una línea recta, una pendiente queda visualizada. Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, la recta se parece más a una recta tangente a la gráfica y su pendiente se parece más a la pendiente de una recta tangente.

Notamos que esta pendiente coincide con la rapidez con que aumenta el valor de la función en cada punto. Dicho de otra manera, si la pendiente en un punto es muy grande, entonces el valor de la función en ese punto crece muy deprisa; si la pendiente es muy pequeña, entonces el valor de la función crece muy despacio en ese punto.

Es decir, tanto la pendiente de la recta tangente como la rapidez de crecimiento en un punto de una función está dado por .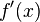

Lamentablemente no todas las funciones poseen derivada, desde el punto de vista geométrico esto se puede deber a varias cosas: por ejemplo hay funciones donde se da el caso de que por un mismo punto pasan muchas rectas tangentes(por ejemplo la función valor absoluto en el punto 0) y no es posible definir de manera única la pendiente a la recta tangente; también se da el caso de que no se puede definir la pendiente a una recta tangente en una función que no es continua; incluso hay funciones donde cualquier recta que pase por uno de sus puntos interseca en una infinidad de puntos muy cercanos y por tanto no hay recta tangente.

Las funciones que poseen derivada se llaman diferenciables.

Conocer la derivada de una función diferenciable por lo general resulta una tarea sencilla utilizando las técnicas de derivación desarrolladas por Gottfried Leibniz e Isaac Newton, las cuales permiten conocer las derivadas de muchas de las funciones de interés frecuente o bien, simplificar el trabajo para encontrar derivadas menos comunes.